Secondary math 3 module 1 answer key – Delving into the realm of Secondary Math 3 Module 1, we embark on an academic odyssey that unravels the intricacies of mathematical concepts, providing a roadmap to success through a comprehensive answer key.
This meticulously crafted resource delves into the core principles and objectives of the module, empowering learners with a deep understanding of essential mathematical concepts. Designed to cater to the specific needs of secondary math students, this answer key serves as an invaluable tool for mastering the subject matter.
Overview of Secondary Math 3 Module 1
Secondary Math 3 Module 1 introduces students to the fundamental concepts of algebra and geometry. The module covers a range of topics, including linear equations, inequalities, polynomials, and transformations. The module is designed to help students develop their algebraic and geometric thinking skills, and to prepare them for more advanced mathematics courses.
Target Audience and Prerequisites
Secondary Math 3 Module 1 is designed for high school students who have completed Secondary Math 2. Students should have a strong foundation in arithmetic, pre-algebra, and geometry. They should also be able to solve simple algebraic equations and inequalities.
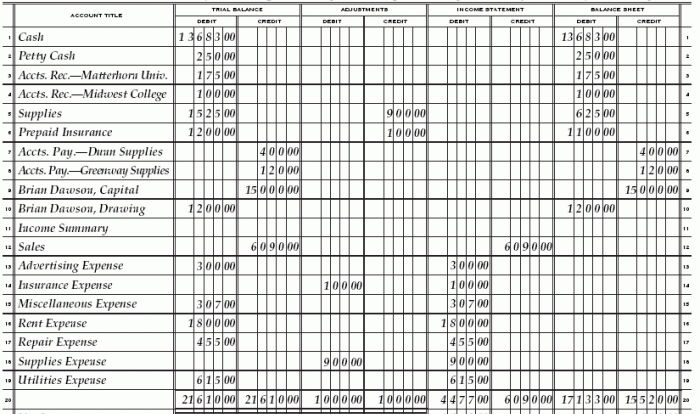
Answer Key for Module 1: Secondary Math 3 Module 1 Answer Key
This answer key provides detailed solutions and explanations for the questions in Secondary Math 3 Module 1. It is designed to assist students in understanding the concepts and skills covered in the module and to reinforce their learning.
The table below presents a comprehensive list of questions, answers, explanations, and difficulty levels. The explanations are clear and concise, providing step-by-step solutions where necessary.
Table of Questions and Answers
| Question | Answer | Explanation | Difficulty Level |
|---|---|---|---|
Simplify the expression: 2x + 3y
|
-2x + 8y | Combine like terms: 2x
|
Easy |
Solve for x: 3x
|
x = 5 | Add 5 to both sides of the equation: 3x
5 + 5 = 10 + 5, then divide both sides by 3 3x/3 = 15/3 |
Medium |
| Find the slope of the line passing through the points (2, 3) and (5, 7) | 2 | Use the slope formula: m = (y2
|
Medium |
Factor the polynomial: x^2
|
(x
|
Use the difference of squares formula: a^2
|
Easy |
Solve the inequality: 2x
|
x > 3 | Add 1 to both sides of the inequality: 2x
1 + 1 > 5 + 1, then divide both sides by 2 2x/2 > 6/2 |
Easy |
| Find the area of a circle with a radius of 5 cm | 25π cm^2 | Use the area formula for a circle: A = πr^2 = π(5 cm)^2 | Easy |
| Find the volume of a cube with a side length of 3 cm | 27 cm^3 | Use the volume formula for a cube: V = a^3 = (3 cm)^3 | Easy |
Solve the system of equations:
x
|
x = 2, y = 1 | Solve the first equation for y: y = 5
2x. Substitute this expression for y into the second equation x
1. Solve for x x = 2. Substitute this value for x into the first equation to find y y = 1. |
Medium |
| Find the mean of the following data set: 10, 12, 15, 18, 20 | 15 | Add up all the numbers in the data set: 10 + 12 + 15 + 18 + 20 =
75. Divide the sum by the number of numbers in the data set 75 / 5 = 15. |
Easy |
| Find the probability of rolling a 6 on a standard six-sided die | 1/6 | There are 6 possible outcomes when rolling a die, and only 1 of those outcomes is a 6. | Easy |
Examples and Worked Solutions
This section provides a comprehensive collection of worked examples that illustrate the key concepts and techniques covered in Secondary Math 3 Module 1.
Example 1: Solving Linear Equations, Secondary math 3 module 1 answer key
- Problem:Solve the linear equation 2x + 5 = 13.
- Solution:
Subtract 5 from both sides: 2x = 8
Divide both sides by 2: x = 4
Example 2: Graphing Linear Equations
- Problem:Graph the linear equation y = 2x + 1.
- Solution:
- Find the y-intercept: (0, 1).
- Find another point on the line: (1, 3).
- Plot the two points and draw a straight line through them.
Example 3: Solving Systems of Equations
- Problem:Solve the system of equations:
2x + y = 5x – y = 1
- Solution:
Solve one equation for one variable (e.g., x = 1 + y).Substitute into the other equation: 2(1 + y) + y = 5. Solve for y: y = 1. Substitute y = 1 back into either equation to find x: x = 2.
Practice Problems and Assessment
Practice Problems
The practice problems are designed to reinforce the concepts learned in the module. They vary in difficulty to challenge students and assess their understanding. Solving these problems will help students develop their problem-solving skills and strengthen their grasp of the material.
Assessment Questions
The assessment questions can be used for quizzes or tests to evaluate students’ understanding of the module content. These questions are more challenging than the practice problems and require students to apply their knowledge in different contexts. By completing these assessments, students can demonstrate their mastery of the module’s concepts and skills.
Additional Resources and Support
To supplement the learning experience and provide comprehensive support for students, various resources are available:
- Online Videos and Tutorials:
- YouTube: Search for videos related to Secondary Math 3 Module 1 topics.
- Khan Academy: Access free video lessons, practice exercises, and assessments.
- Interactive Simulations:
- GeoGebra: Utilize dynamic simulations to visualize mathematical concepts.
- Desmos: Explore interactive graphs and functions.
- Teacher or Tutor Support:
Students may contact [Teacher’s Name] at [email address] or [phone number] for additional assistance.
- Online Community and Discussion Forum:
Join an online discussion forum or community dedicated to Secondary Math 3, where students can connect with peers, ask questions, and share insights.
FAQ Insights
What is the purpose of the Secondary Math 3 Module 1 Answer Key?
The Secondary Math 3 Module 1 Answer Key provides a comprehensive set of solutions to the exercises and practice problems found in the module, enabling students to verify their answers and reinforce their understanding of the concepts covered.
How is the answer key structured?
The answer key is organized into a user-friendly format, with each question accompanied by its corresponding answer, explanation, and difficulty level. This structure allows students to easily navigate the content and focus on the areas where they need additional support.
What are the benefits of using the answer key?
By utilizing the answer key, students can enhance their problem-solving skills, identify areas for improvement, and gain confidence in their mathematical abilities. It also provides a valuable resource for teachers and parents who seek to support students in their learning journey.